MTH243
Statistics Notes on Describing Data
Spring 2022

Chapter 2 Describing Data

§ 2.1 Categorical Data

  • Categories
  • Frequency, count
  • Proportion, relative frequency
  • Bar/Column Chart
  • Pie Chart
  • Notation for a Proportion
  • Two-way tables for two categorical variables
  • Multiple proportions in two-way tables
    • total proportions
    • row proportions
    • column proportions
  • Difference in proportions
  • Comparative column charts
49% of Americans say affordable housing is a major problem in their area. Pew Research 2021

§ 2.2 One Quantitative Variable: Shape and Center p.72 (<1hr)

Key Concepts

  • Use a dotplot or histogram to determine the shape of a distribution
  • Understanding and calculating mean and median
  • Identify the approximate locations of the mean and the median on a dotplot or histogram
  • Understanding the impact of skewness and outliers on the mean and median
What is a distribution?

Data set examples

For each quantitative variable:

  • Make a dot plot with StatKey
  • Make a histogram with StatKey
  • Make another histogram with StatKey
  • Copy one of these on paper and plot the mean and median.
Frequency Tables and Histograms
  • Frequency Table
    • 6 to 20 classes
    • Decide on number of class; find start and width
    • Classes should be the same width
    • There is no "best" histogram
  • Relative and Cumilative frequency
    TemperatureCountRelativeCumulative
    96.4 ≤ x < 96.8211/250.04
    96.82 ≤ x < 97.2466/250.28
    97.24 ≤ x < 97.6633/250.4
    97.66 ≤ x < 98.0866/250.64
    98.08 ≤ x < 98.566/250.88
    98.5 ≤ x < 98.9233/251
Shapes of Distributions

The skew is to the tail.

  • Symmetrical
    mean `~~` median
  • Skewed left
    mean < median
  • Skewed right
    mean > median
Measures of Center
  • `bar(x)` = Mean = Arithmetic Mean = Average = Sum / Count
    spreadsheet function =AVERAGE(data)
  • `m` = Median = middle when ranked
    locator = `(n+1)/2`
    spreadsheet function =MEDIAN(data)
  • Mode = most frequently occurring = good for qualitative data, among others
  • The Law of Large Numbers and the Mean
    Larger samples and/or repeated sampling will get `barx` closer to `mu`.
  • Interpreting the mean
    • Context
    • The average human body temperature is 97.6.
      OK.
    • The average U.S. household has 2.53 people. (ref)
      Wait. How can you have half of a person?
      Right. OK.
      The average U.S. household has between 2 and 3 people.
      Thanks

§ 2.3 One Quantitative Variable: Measures of Spread

  • Use technology to compute summary statistics for a quantitative variable
  • Recognize the uses and meaning of the standard deviation
  • Compute and interpret a z-score
  • Interpret a five number summary or percentiles
  • Use the range, the interquartile range, and the standard deviation as measures of spread
  • Describe the advantages and disadvantages of the different measures of center and spread
  • `s` = Standard Deviation of a Sample = `sqrt((sum (x-barx)^2)/(n-1))`
    spreadsheet function =STDEV(data) or =STDEV.S(data)
  • `sigma` = Standard Deviation of a Population
  • Range = max - min
  • Examples: Mortality Rate by Country, in Sheets, Docs, StatKey, other
  • Counting StDs and z-scores
  • Can standard deviation help us find outliers? Unusual values?
    We consider the extreme 5% of the data, this is often outside 2 standard deviations from the mean.

§ 2.4 Box Plots and Quantitative/Categorical Relationships

Goals

  • Identify outliers in a dataset based on the IQR method
  • Use a boxplot to describe data for a single quantitative variable
  • Use a side-by-side graph to visualize a relationship between quantitative and categorical variables
  • Examine a relationship between quantitative and categorical variables using comparative summary statistics
  • Percentiles with Quantitative Data
    • Percentile
    • Percentile location, aka data index/position
    • Percentile value
  • Examples
    • P10 is the 10th percentile, that is, the position in the data set were 10% of the data is at or below that point.
    • Suppose we have a sample of size n=20. Then the position of P10 is 0.10*(20+1)=2.1, or the number in the 2nd position when ranked.
    • Consider the Presidents ages:
      Example: Age at Inauguration of 20th Century US Presidents
      42, 43, 46, 47, 51, 51, 51, 52, 54, 54, 55, 55, 56, 56, 60, 61, 62, 64, 69, 70
      So, P10=43
      According to MS Excel or Google Sheets, P10 = PERCENTILE.INC(data,0.1) = 45.7
      Close, but different from my method. There are other ways to identify percentile values that will be close to but different from each of these.
      Oh, well.
  • Quartile
    • percentiles
    • locators
    • 5 different quartiles
    • Quartile vs Quarter
  • Interpretaion
    Statistic Construction Teacher
    min 30 21
    Q1 35 30
    m 40 35
    Q3 42 40
    Max 46 43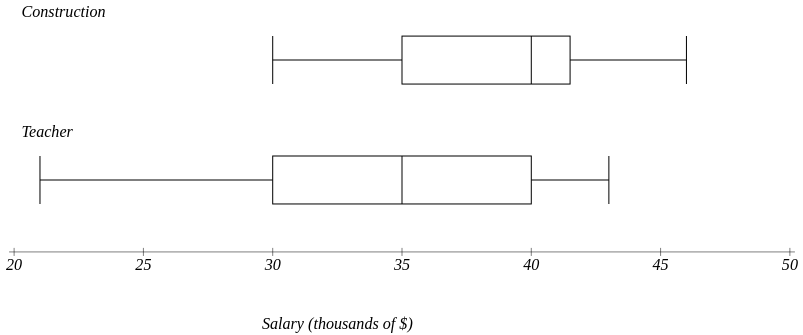
    box plot comparison
  • 5 number summary and the Box Plot
  • Extended InterQuartile Range
    aka Outlier Fences, lower and upper
    Lower Fence = `Q_1-1.5*IQR`
    Upper Fence = `Q_3+1.5*IQR`
    These values fence in "usual" data, hence give us a measure for outliers, aka, "unusual" data.

§ 2.Two Quantitative Variables: Scatterplot and Correlation

§ 2.6 Two Quantitative Variables: Linear Regression

§ 2.Data Visualization: Multiple Variables