MTH212
Notes on Number Theory and Fractions
Winter 2019
Chapter 4 Number Theory
§ 4-1 Divisibility
`b` divides `a`, `b|a`, if and only if, there is a `q` such that `a=b*q`.
for example
- `2|6` since `6=2*3`
- `6 cancel{|} 2`
- `0|2`
- `2|4n` for all whole numbers `n`
Divisibility Rules
- If `d | a` and `d | b`, then `d | (a+b)`.
Ex: `3|6` and `3|9`, so `3|15` - If `d | a` and `d cancel{|} b`, then `d cancel{|} (a+b)`.
Ex: `3|6` and `3 cancel{|} 10`, so `3 cancel{|} 16` - If `d | a` and `d | b` and `a>=b`, then `d | (a-b)`.
- If `d | a` and `d cancel{|} b` and `a>=b`, then `d cancel{|} (a-b)`.
- If `d cancel{|} a` and `d | b` and `a>=b`, then `d cancel{|} (a-b)`.
Divisibility Tests
- 2
- the ones digit is a `0,2,4,6,8`
- 3
- the sum of the digit is a multiple of 3
- 4
- the two right-most digits form a multiple of 4
- 5
- the ones digit is a `0,5`
- 6
- meets the tests for 2 and 3
- 8
- the three right-most digits form a multiple of 8
- 9
- the sum of the digit is a multiple of 9
- 10
- the ones digit is a `0`
- 11
- the difference between the sum of the digits from the even powers of 10 and the sum of the digits from the odd powers of 10, is a multiple of 3
§ 4-2 Primes and Composites
Consider the image below:
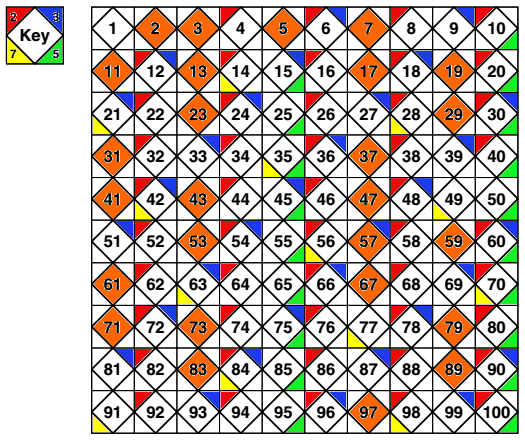
The corners show divisibility by 2, 3, 5, and 7. Numbers with any colored corners are composite. Orange numbers are prime.
Terminology
- Divisor
- a number that is a factor of another number
`b` divides `a`, `b|a`, if and only if, there is a `q` such that `a=b*q`. - Factor
- a number that is a divisor of another number
- Multiple
- the product of a given number with any whole number
- Prime
- exactly two distinct divisors
- Composite
- more than two distinct divisors
- Factorization
- write as a product of whole numbers
- Prime Factorization
- write as a product of only prime numbers
- Factor Trees
- factor a number as a pair of factors; repeat with each factor until only prime numbers remain.
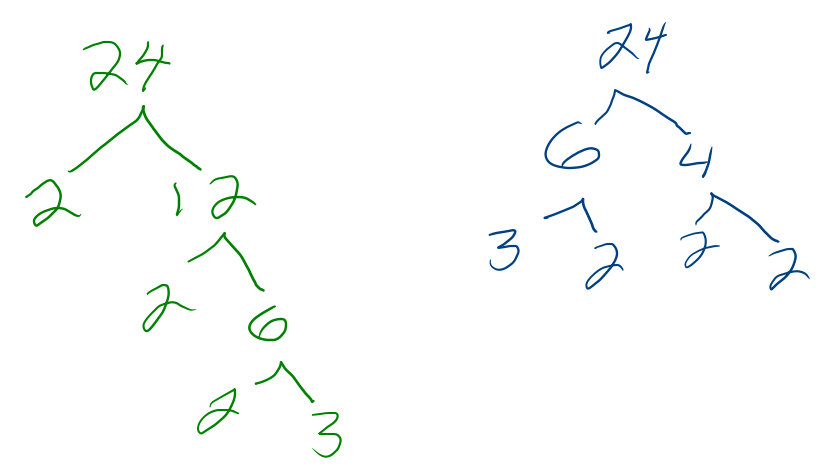
§ 4-3 Greatest Common Divisor and Lowest Common Multiple
GCD methods
The List Method:
Consider 24 and 18:
List the factors of each number.
24: 1, 2, 3, 4, 6, 8, 12, 24
18: 1, 2, 3, 6, 9, 18
18: 1, 2, 3, 6, 9, 18
Identify the common factors.
1, 2, 3, 6
6 is the greatest of the common factors.
The Color Rod Method:
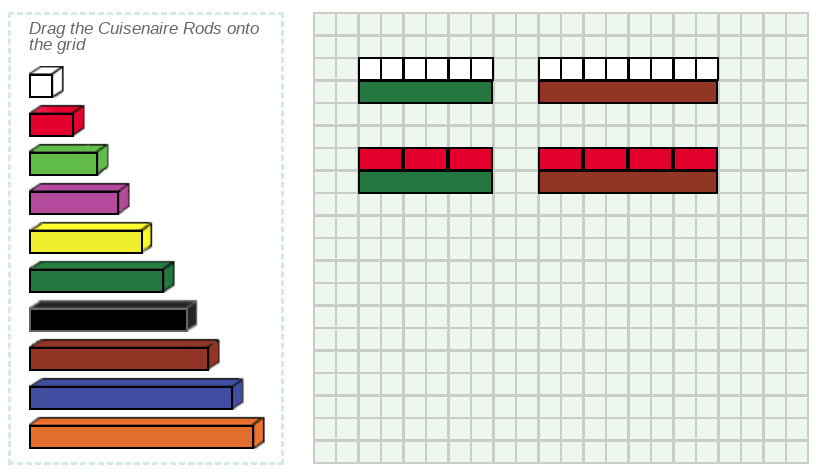
The Prime Factorization Method:
Consider 24 and 18:
Find the prime factorization of each number.
`24 = 2^3*3`
`18 = 2*3^2`
`18 = 2*3^2`
Select the lowest power of each common prime to multiply.
`2*3 =6`
The Euclidean Algorithm:
Consider 24 and 18:
Repeated division of a sort
`24 = 18*1+6`
`18 = 6*3+0`
`18 = 6*3+0`
SOnce you get a zero remainder, the previous remainder must be the GCF.
GCF `=6`