MTH062 Quant Lit 1

Fun with big numbers, analyzing rates of change, and formulas.
Module 1
§ 1-1 Intro to Quantitative Reasoning
Every year since 1950,
the number of American children
gunned down has doubled.
I am guessing that about 25 children where gunned down in 1950.
How many where gunned down in 1960, if the statement above is true?
I think that I would have to double 25 ten times, since 1960 is ten years later.
`25*2*2*2*2*2*2*2*2*2*2=25,600`
So, if there were 25 children gunned down in 1950, then there were 25,600 children gunned down in 1960.
What about 1970?
`25600*2*2*2*2*2*2*2*2*2*2=26,214,400`
Uh oh, that is a lot of children!!!
Significant Figures
"Significant figures" is an idea that helps us figure out what place to round at.
The rule of significant figures is that the answer can have _no more_ digits than the _fewest_ digits of each number you started with.
Applying significant figure to this situation, since I started with 25 children, I have two significant figures.
| Year | Number of Children | Rounded using words |
|---|---|---|
| 1950 | 25 | twenty-five |
| 1960 | 26,000 | twenty-six thousand |
| 1970 | 26,000,000 | twenty-six million |
§ 1-2 Eighteen Trillion and Counting
How big is a billion or a trillion?
So, where on the number line is 1 billion? Make a mark for 1 billion on the number line.
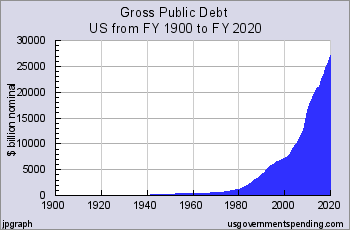
In news about politics and government, BIG numbers are talked about often. Below is a chart showing the national deficit over time.
On a scale from 0 to 1 trillion, 1 billion is very close to zero, since 1 trillion is 1000 billion!
Imagine a stack of 1,000 one‐dollar bills, which is about 4.3 inches tall.
Complete the table below:
| $ Amount | Height (inches) | Height (feet) | Height (miles) |
|---|---|---|---|
| $1,000 | 4.3 | ||
| $1 million | 4,300 | 358 | |
| $1 billion | 4,300,000 | 358,333 | 68 |
| $1 trillion | 4,300,000,000 | 358,333,333 | 68,866 |
This means that a stack of $1 bills, 3.5 trillion high, would reach the moon.
Significant Figures
"Significant figures" is an idea that helps us figure out what place to round at.
The rule of significant figures is that the answer can have _no more_ digits than the _fewest_ digits of each number you started with.
In the table above, we started with one stack of 1000 $1 bills that is about 4.3 inches tall. We then end up with 1 billion of those stacks to end up with $1 trillion.
Since 1000 dollar bills is about, but not exactly 4.3 inches, we can't really be sure that 1 trillion dollar bills is exactly 358,333,333 feet tall or exactly 68,866 miles tall.
The idea of significant figures is that we are only confident about 2 digits, that is the 4.3 inches. So calculations based on that might only be accurate to 2 digits.
This means that the stack of 1 trillion dollars is about 69,000 miles tall if we round to 2 significant figures. There are some situations where we would truncate 68,866 to 2 significant figures as 68,000.
§ 1-3 Algebra and Scientific Notation with Small Numbers
Students will understand that
- in algebra, numbers and variables can be combined to produce expressions, equations and inequalities.
- numbers between 0 and 1 can be written using scientific notation. The exponent will be negative.
Students will be able to
- distinguish between expressions, equations and inequalities.
- convert between standard and scientific notation.
- multiply and divide using scientific notation, both by hand and with a calculator.
- apply the rules of exponents to variables.
Lesson
Rank these from Largest to smallest
| Distance from earth to the moon | Kitchen counter height from floor, baseball bat, walking stick | Size of a chromosome or red blood cell |
| Distance from earth to Mars (at their closest point) | Size of a water molecule or carbon atom | One trip around Lake Waughop |
| Distance from earth to the sun | Size of a virus | Distance from earth to space station |
| Length of a grain of rice | Distance from earth to Pluto (at their closest point) |
Significant Figures
"Significant figures" is an idea that helps us figure out what place to round at.
Suppose we need to multiply 3.25 by 6.7
3.25*6.7 = 21.775
The rule of significant figures is that the answer can have _no more_ digits than the _fewest_ digits of each number you started with.
3.25 has 3 digits.
6.7 has 2 digits.
So I have to round my answer to 2 digits.
21.775 is about 22 to two significant figures.
§ 1.4 Water Footprint
Specific Objectives
Students will understand that
- the magnitude of large numbers is seen in place value and in scientific notation.
- proportions are one way to compare numbers of varying magnitudes.
- different comparisons may be needed to accurately compare two or more quantities.
Students will be able to
- express numbers in scientific notation.
- calculate ratios of large numbers.
- use multiple computations to compare quantities.
- compare and rank numbers including those of different magnitudes (millions, billions).
Prep
- Fractions
- Decimals
- Percents
- Scientific Notation
- Problem: Water usage varies greatly in different countries, from as little as 20 liters a day per person in some third world countries, to 600 liters a day in the U.S. How much water would be needed for one day if every person in the world used 50 liters of water a day, and the population of the world was about `6.93×10^9`, as it was in 2010?
- Exponent Rules
Videos
Lesson
| Country | Population (millions) | Total Water Footprint billions of cubic meters per year |
water/person in cubic meters |
|---|---|---|---|
| China | 1,346 | 1,368 | |
| India | 1,241 | 1,144 | |
| U.S. | 312 | 812 |
HW
Order of operations and parenthesis
Calculate your Water footprint: Water Calculator
§ 1.5 Dimensional Analysis
Specific Objectives
Students will understand that
- units provide meaning to numbers in a context.
- the units in an expression may be used as a guide for needed conversions.
Students will be able to
- use units to determine which conversion factors are needed for dimensional analysis.
- use dimensional analysis to convert units and rates.
Prep
- Multiplying fractions
`3/4*2/15=(cancel3 1)/(4)*(2)/(cancel15 5)=(1)/(cancel4 2)*(cancel2 1)/(5)=1/10` - Dividing fractions
`2/3-:1/2=2/3xx2/1` - Conversion facts
1 foot = 12 inches or `(1" foot")/(12" inches")=1`
Videos
Lesson
|
Unit Equivalencies |
||
|
USCS (US Customary System) |
USCS – Metric |
Metric or SI |
|
Length |
||
|
12 inches (in) = 1 foot (ft) 3 feet (ft) = 1 yard (yd) 1760 yards (yd) = 1 mile (mi) 5280 feet (ft) = 1 mile (mi) |
1 inch (in) = 2.54 centimeters cm) 0.62 miles (mi) = 1 kilometer (km) |
1000 millimeters (mm) = 1 meter (m) 1000 meters (m) = 1 kilometer (km) 100 centimeters (cm) = 1 meter (m) |
|
Area |
||
|
1 square mile (mi2)= 640 acre (ac) 1 acre (ac) = 43,560 square feet (ft2) |
2.471 acre (ac) = 1 hectare (ha) 1 square mile (mi2) = 2.59 square kilometers (km2) |
1 square kilometer (km2) = 100 hectare (ha) 1 hectare (ha) = 10,000 square meters (m2) |
|
Volume |
||
|
8 ounces (oz) = 1 cup (c) 2 cups (c) = 1 pint (pt) 2 pints (pt) = 1 quart (qt) 4 quarts (qt) = 1 gallon (gal) |
1 quart (qt) = 0.946 liters (L) |
1000 milliliters (ml) = 1 liter (L) 1000 liters (L) = 1 cubic meter (m3) |
|
Weight or Mass |
||
|
16 ounces (oz) = 1 pounds (lb) 2000 pounds (lb) = 1 ton |
2.20 pounds (lb) = 1 kilogram (kg) 1 pound (lb) = 453.6 grams (g) |
1000 milligrams (mg) = 1 gram (g) 1000 grams (g) = 1 kilogram (kg) 1000 kilograms = 1 metric ton |
§ ?-? Title
Specific Objectives
Students will understand that
- Item
Students will be able to
- Item
Prep
- Item
Videos
Lesson
§ 1.6 The Cost of Driving
Specific Objectives
Students will understand that
- units can be used as a guide to the operations required in the problem—that is, factors are positioned so that the appropriate units cancel.
- the units required in a solution may be used as a guide to the operations required.
Students will be able to
- write a rate as a fraction.
- use dimensional analysis to determine the factors in a series of operations to obtain solutions.
- solve a complex problem with multiple pieces of information and steps.
Prep
- Equivalent Fractions
Videos
Lesson
Module 2
§ 2-1 A Taxing Set of Problems
Problem Situation: Calculate income tax for tax bracket
| If Taxable Income Is: | The Tax Is: |
|---|---|
| Not over $18,150 | 10% of the taxable income |
| Over $18,150 but not over $73,800 | $1,815 plus 15% of the excess over $18,150 |
| Over $73,800 but not over 148,850 | $10,162.50 plus 25% of the excess over $73,800 |

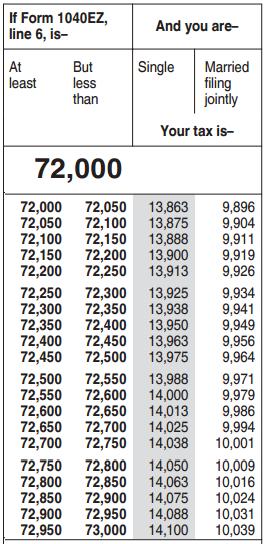
Suppose a couple, married with no kids, filing jointly, earned $93,000 with no other interest or income.
Based on the standard standard married filing jointly deduction, their taxable income is `$93,000-$20,300=$72,700`
According to the tax table above their income tax is
`$1,815+0.15*($72,700-$18,150)=``$9,997.50`
Compare this to line 15 of the table below: