MTH211 Foundations of Elementary Math 1

the one percent

Fun with whole numbers.

MTH211
Notes on Whole Numbers
Fall 2019

Table of Contents

§ 3.2 Addition and Subtraction

Math Activity 3.2: Playing with Blocks

Addition with base-ten blocks
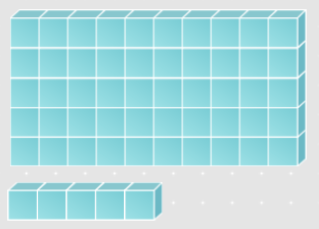
22 plus 23 sum of 55

Math Activity 3.2: Playing with Blocks

Subtraction with base-ten blocks

36 - 23 means, what do you get if you take 23 away from 36?

So, start with 36:

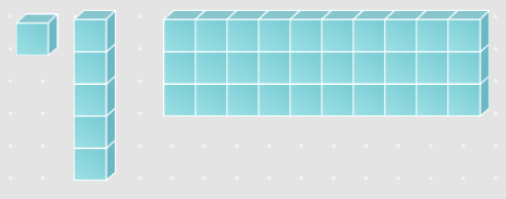
36 in base-ten blocks

Now, take away 23:

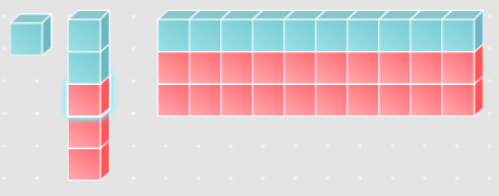
36 take away 23 in base-ten blocks

That leaves 13!

Main topics
  • Addition Models
    • set model
    • number line model
  • Addition Properties
    • closure
    • Commutative
    • Associative
    • identity
  • Addition Algorithms
    • standard (right to left, regroup)
    • Expanded
    • Lattice
    • Hindu (left to right)
  • Inequality
  • Subtraction Models
    • Take-away
    • Compare
    • Missing Addend (what do I add?)
    • number line
  • Subtraction Algorithms
    • Standard (right to left, rename)
    • Equal Additions
    • Hindu (left to right)
    • Complements
    • Subtract up
    • low stress
  • Approximations and Estimations
    • Front end
    • Compatible numbers

§ 3.3 Multiplication

Math Activity 3.3: Multiplication as Area
an array of squares, 23 by 12, with rows 10 tall and 2 tall, and columns 10 wide, 10 wide, and 3 wide.

Main Topics
  • Multiplication Models
    • Groups of
    • Repeated Addition
    • Area
    • Array
    • Cartesian Product
  • Factors
  • Products
  • Partial Products
  • Algorithms
    • Repeated addition
    • Expanded
    • Regrouping (Standard)
    • Hindu (left to right)
    • Lattice
  • Properties
    • Closure
    • Commutative
    • Associative
    • Identity (one)
    • Distributive property of multiplication over addition
  • Estimation

§ 3.4 Division and Exponents

Math Activity 3.4: Division Models

Check out section 3.4 of the book, Division and Exponents. There are 2 models listed:

1. The Set Partition Model (sharing concept)

2. The Repeated Subtraction Model (measurement concept)

For each of these illustrate and explain 42/3. Your illustrations should be similar to those in the book for Example D, 48/4.

Main topics
  • Definition of division:
    If `n-:d=q`, then `q*d=n`
    `6-:2=3` since `3*2=6`
  • Division Models
    • Set Partition
      Split 6 into 2 groups. How many are in each group?
      6 is 2 groups of 3, set Partition model for division
    • Repeated Subtraction
      How many groups of 2 are in 6?
      6 is 3 groups of 2, repeated subtraction, aka groups in
    • Missing Factor (aka what do I multiply by?)
      `6-:2=square` means `square xx 2 = 6`
  • Division Algorithms
    • Repeated Subtraction
    • Grouped Repeated Subtraction
    • Scaffolding
    • Long Division
    • Short Division
  • Division Algorithm Theorem
    For any whole numbers `n` and `d`, with divisor `d!=0`, there are whole numbers `q` and `r` such That
    • `n=d*q+r`
    • `0≤r<d`
  • Division with zero
    • `0//3=0`
    • `3//0` is undefined
    • `0//0` is indeterminate
  • Equal quotients
    `70-:20=7-:2=3 1/2`
  • Approximate quotients and compatible numbers
    `31-:16~~30-:15=2`
  • Rounding and front-end estimation
    `723-:215~~700-:200=7-:2=3 1/2`
  • Exponents
    • `b^0=1` show pattern
    • `b^1=b` show pattern
    • `a^n*a^m=a^(n+m)`
    • `a^n/a^m=a^(n-m)`
    • `(a^n)^m=a^(n*m)`
    • `(a*b)^n=a^n*b^n`
    • `(a/b)^n=a^n/b^n`
  • Scientific Notation
  • Order of Operations
    1. Parentheses (inside)
    2. Exponents
    3. Multiplication OR Division (left to right)
    4. Addition OR Subtraction (left to right)

Chapter 4: Number Theory

§ 4.1 Factors and Multiples

Math Activity 4.1: ?

§ 4.2 Greatest Common Factor and Least Common Multiple

Math Activity 4.2: ?