Notes on Differential Calculus

Winter 2021

Chapter 2

§ 2.1 A Preview of Calculus

Learning Outcomes

• Describe the tangent problem and how it led to the idea of a derivative.
• Explain how the idea of a limit is involved in solving the tangent problem.
• Recognize a tangent to a curve at a point as the limit of secant lines.
• Identify instantaneous velocity as the limit of average velocity over a small time interval.
• Describe the area problem and how it was solved by the integral.
• Explain how the idea of a limit is involved in solving the area problem.
• Recognize how the ideas of limit, derivative, and integral led to the studies of infinite series and multivariable calculus.

The Tangent Line Problem

How do we find the slope of a curve at a point when we need two points to find a slope?

Geogebra Secant Example
Geogebra Spreadsheet Example

The Area Problem

Consider the image below:

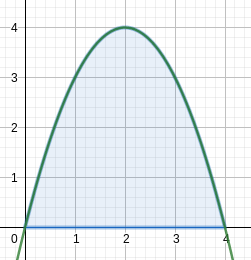
Positive area under a curve.

How do we find such an area?

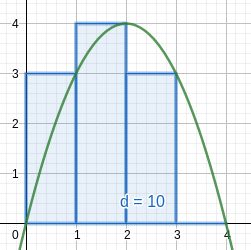
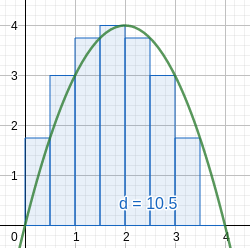
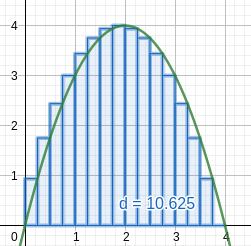
Rectangles are easy to work with.

§ 2.2 The Limit of a Function

Text for Section 2.2 The Limit of a Function

Learning Outcomes

• Using correct notation, describe the limit of a function.
• Use a table of values to estimate the limit of a function or to identify when the limit does not exist.
• Use a graph to estimate the limit of a function or to identify when the limit does not exist.
• Define one-sided limits and provide examples.
• Explain the relationship between one-sided and two-sided limits.
• Using correct notation, describe an infinite limit.
• Define a vertical asymptote.

Intuitive Definition of a Limit

The Existence of a Limit

One Sided Limits

Infinite Limits

§ 2.3 Limit Laws

Text for Section 2.3 The Limit Laws

Learning Outcomes

• Recognize the basic limit laws.
• Use the limit laws to evaluate the limit of a function.
• Evaluate the limit of a function by factoring.
• Use the limit laws to evaluate the limit of a polynomial or rational function.
• Evaluate the limit of a function by factoring or by using conjugates.
• Evaluate the limit of a function by using the squeeze theorem.

The basics

• `lim_{x to a} C = C`
• `lim_{x to a} x = a`

The Laws

Assumptions: `f(x)` and `g(x)` are defined for an interval of numbers containing `x=a`, but maybe not at `a`. Each function has a limit at `x=a`. `lim_{x to a} f(x)=L` and `lim_{x to a} g(x)=M`.

• `lim_{x to a}c*f(x)=c*lim_{x to a}f(x)=cL`
• `lim_{x to a}(f(x)+-g(x))=lim_{x to a}f(x)+-lim_{x to a}g(x)=L+-M`
• `lim_{x to a}(f(x)*g(x))=lim_{x to a}f(x)*lim_{x to a}g(x)=L*M`
• `lim_{x to a}(f(x)/g(x))=(lim_{x to a}f(x))/(lim_{x to a}g(x))=L/M`
• `lim_{x to a}(f(x))^n=(lim_{x to a}f(x))^n=L^n`
• `lim_{x to a}root(n){f(x)}=root(n){lim_{x to a}f(x)}=root(n){L}`

NOTE: It is very important that these laws only apply if each function actually has a limit. Limits of infinity do NOT exist.

Examples

Consider one-sided limits like `lim_{x to 2^-)sqrt(x-2)`

Consider piece-wise functions with two-sided limits.

The Squeeze Theorem

`lim_{x to 0}sin(x)/x`

Other examples

`lim_{theta to pi} sin(theta)/tan(theta)`

§ 2.4 Continuity

Text for Section 2.4 Continuity

Learning Objectives

• Explain the three conditions for continuity at a point.
• Describe three kinds of discontinuities.
• Define continuity on an interval.
• State the theorem for limits of composite functions.
• Provide an example of the intermediate value theorem.

Continuity at a point

A function f(x) is continuous at a point a if and only if the following three conditions are satisfied:

1. `f(a)` is defined.
2. `lim_{x to a} f(x)` exists.
3. `lim_{x to a} f(x)=f(a)`

Types of discontinuities

• Removable
• Jump
• Infinite

Continuity over an interval

A function `f(x)` is continuous over an open interval `(a, b)` if it is continuous at each point in the interval.

A function f(x) is said to be continuous from the right at a if `lim_{x to a^+}f(x)=f(a)`.

A function f(x) is said to be continuous from the left at a if `lim_{x to a^-}f(x)=f(a)`.

The intermediate value theorem

Let f be continuous over a closed, bounded interval [a,b]. If z is any real number between f(a) and f(b), then there is a number c in [a,b] satisfying f(c)=z.